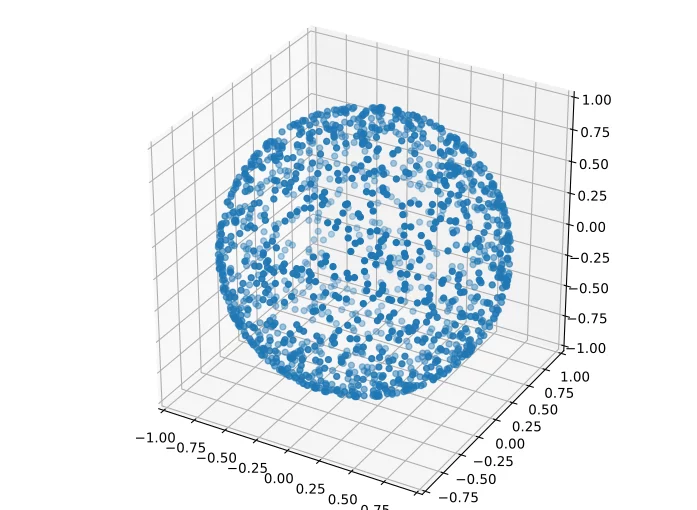
This question often pops up, when you need a random direction vector to place things in 3D or you want to do a particle simulation.
We recall that a 3D unit-sphere (and hence a direction) is parametrized only by two variables; elevation \theta \in [0; \pi] and azimuth \varphi \in [0; 2\,\pi] which can be converted to Cartesian coordinates as
\begin{aligned} x &= \sin\theta \, \cos\varphi \\ y &= \sin\theta \, \sin\varphi \\ z &= \cos\theta \end{aligned}If one takes the easy way and uniformly samples this parametrization in numpy like
phi = np.random.rand() * 2 * np.pi
theta = np.random.rand() * np.piOne (i.e. you as you are reading this) ends with something like this:
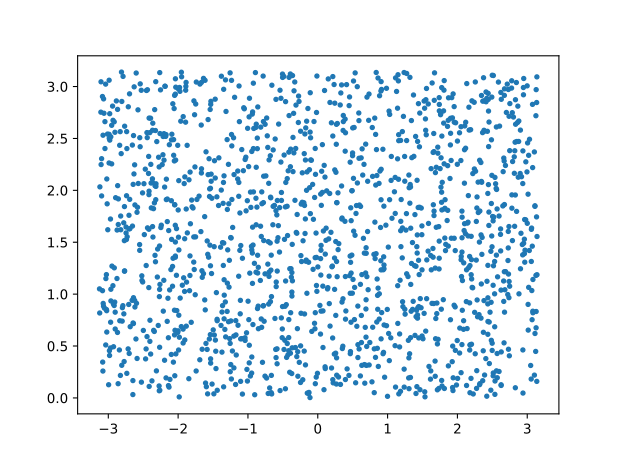
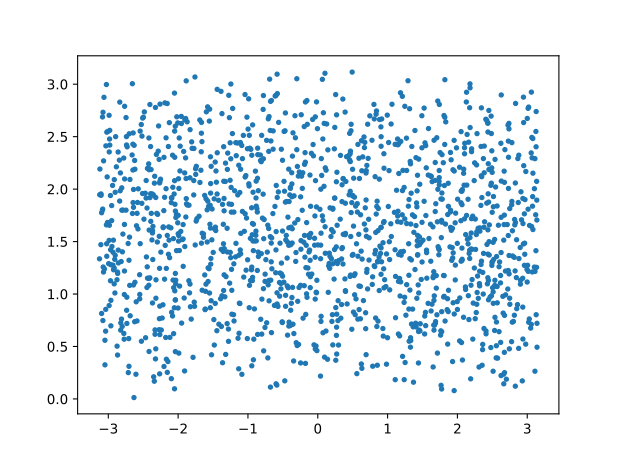
While the 2D surface of polar coordinates uniformly sampled (left), we observe a bias of sampling density towards the poles when projecting to the Cartesian coordinates (right).
The issue is that the cos mapping of the elevation has an uneven step size in Cartesian space, as you can easily verify: cos^{'}(x) = sin(x).
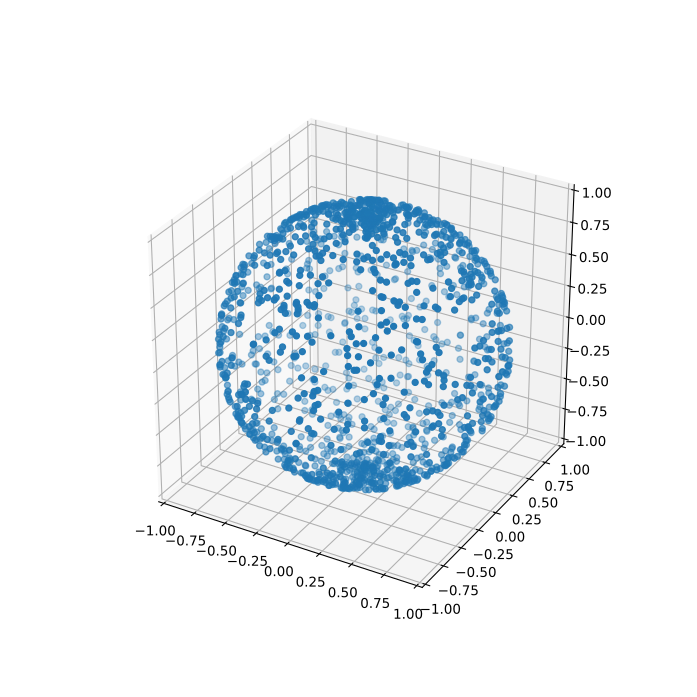
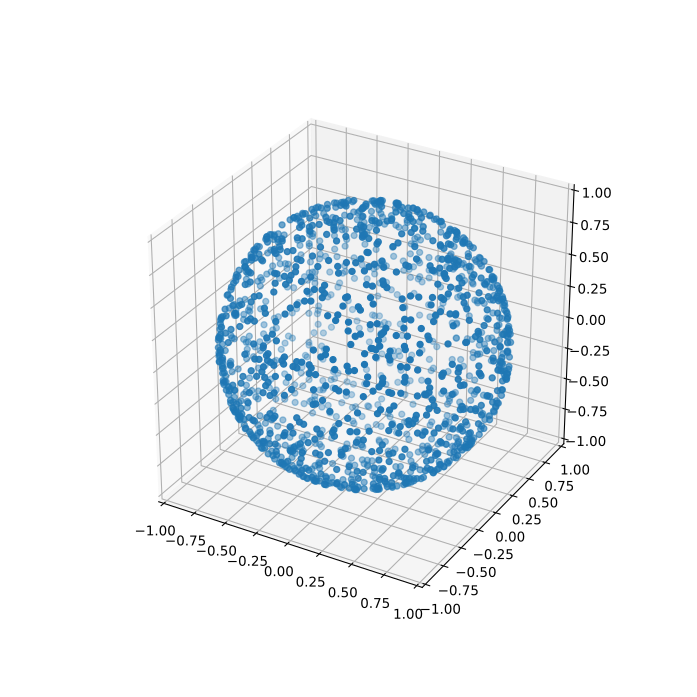
The solution is to simply sample the elevation in the Cartesian space instead of the spherical space – i.e. sampling z \in [-1; 1]. From that we can get back to our elevation as \theta = \arccos z:
z = 1 - np.random.rand() * 2 # convert rand() range 0..1 to -1..1
theta = np.arccos(z)As desired, this compensates the spherical coordinates such that we end up with uniform sampling in the Cartesian space:
Custom opening angle
If you want to further restrict the opening angle instead of sampling the full sphere you can also easily extend the above. Here, you must re-map the cos values from [1; -1] to [0; 2] as
cart_range = -np.cos(angle) + 1 # maximal range in cartesian coords
z = 1 - np.random.rand() * cart_range
theta = np.arccos(z)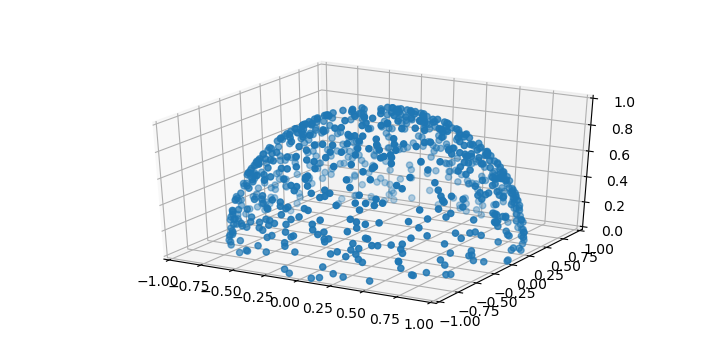
Optimized computation
If you do not actually need the parameters \theta, \varphi, you can spare some trigonometric functions by using \sin \theta = \sqrt { 1 - z^2} as
\begin{aligned} x &= \sqrt { 1 - z^2} \, \cos\varphi \\ y &= \sqrt { 1 - z^2} \, \sin\varphi \end{aligned}